> with(LinearAlgebra):

> K := Matrix([[-k1-k2,0,0,0],[+k1,0,0,0],[+k2,0,-k3,+k4],[0,0,+k3,-k4]]);

> E := Eigenvectors(K);

> v := E[1];

> X := E[2];

> L := DiagonalMatrix([exp(v[1]*t),exp(v[2]*t),exp(v[3]*t),exp(v[4]*t)]);

> c0 := Vector ([Ao,0,0,0]);

> ct := X . L . MatrixInverse(X) . c0;

> ctA := ct[1];

> ctB := ct[2];

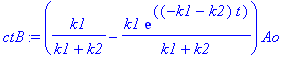
> ctC := ct[3];

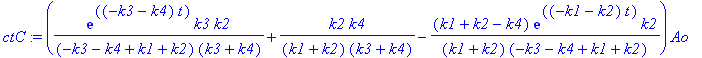
> ctD := ct[4];

>
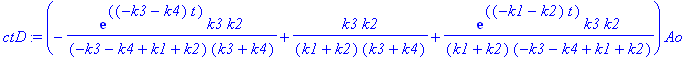